Topological qubits

This work has been done in collaboration with B. Douçot (LPTHE, Paris) and L. Ioffe (Ruttgers University, USA).
The practical implementation of a quantum computer is hindered by several problems due to the fragility of quantum systems. In order to solve this problem, it has been proposed in 1997 to use systems with topological properties (\emph{i.e.} properties related to geometry) which would guarantee the fidelity. Following the same idea, one can use the topological properties of the system to realize a qubit which would be stable against perturbations.
As quantum objects, qubits are very sensitive to outside perturbations. Thus, qubits in condensed matter systems such as Josephson junctions have lifetimes of some microseconds while qubits realized in trapped ions systems can have a lifetime of some tens of seconds. If this second time might seem long, it decreases very rapidly as the number of qubits becomes large which is necessary if one wishes to perform a "useful" calculation (such as the factorization of a number containing hundreds of bits). This is due to an unavoidable coupling with the environment, which is responsible for the loss of quantum properties, decoherence.
In order to limit decoherence, one may use the idea of topological protection. The system is thus built to have topological properties which will limit the effects of decoherence. In order to achieve this, one considers an array of N by N spins verifying two properties:
the system displays a large number of symmetries which leads to the existence of two degenerate fundamental levels.
the system has a large energy gap, that is the distance in energy between the fundamental levels and the first excited levels is "large".
Most noises are local in the sense that they only affect a single spin at a time: thus, they will only break one symmetry while the remaining symmetries will guarantee the energy stability of the qubit states. The decoherence rate, Gd, then becomes (Gd/D)N where D is the energy gap.
This idea had been initially proposed with Josephson junctions with an interaction between nearest neighbors. We have studied its implementation with an infinite range interaction between trapped ions on a square lattice. This interaction is realized by two non resonant laser beams and has already been used to create an entangled state of an ion chain.
The advantage of an infinite range interaction is that the energy gap does not vanish rapidly as the size of the system increases as is the case with a short range interaction.
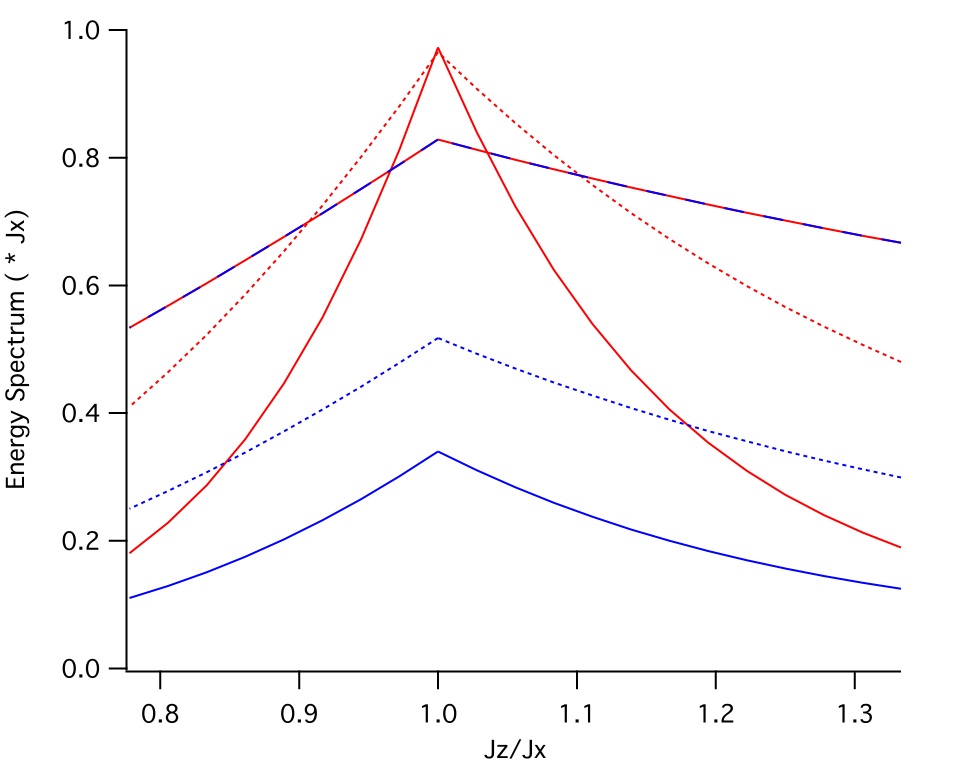
Energy gap as a function of the ratio between the interaction strength along the lines (Jx) and along the rows (Jy) for short range (blue) and long range (red) and three systems sizes (2x2, long dashed; 3x3 short dashed and 4x4, continuous line). The gap does not decrease significantly between the various system sizes for the infinite range interaction.
Surface microtraps allow for a wide range of confinement geometries which can be controlled by the application of electric potentials (\emph{e.g.}, S. Seidelin, et al., "A microfabricated surface-electrode ion trap for scalable quantum information processing, Phys. Rev. Lett. 96, 253003 (2006)). One can thus envision, with current technologies, to realize several parallel surface traps which would confine the ions in a periodic trap. The ions confined in a given trap would strongly interact with each other due to the Coulomb force while ions confined in different traps would be independent because of the large transverse stiffness of the microtraps. By combining two orthogonal arrays on a single chip, one can alternate between two configurations, one where the ions in a row interact and one where the ions in a column interact, thus realizing the required hamiltonian.
More information can be found in the following papers:
Initial idea of topological quantum computing: A. Kitaev, "Fault tolerant quantum computation by anyons", Ann. Phys. 303, 2-30 (2003), originally published in quant-ph/970702
Qubits protected topologically against decoherence: B. Douçot, M.V. Feigel'man, L.B. Ioffe, and A.S. Ioselevich, "Protected qubits and Chern-Simons theories in Josephson junction arrays", Phys. Rev. B 71 024505 (2005)
Infinite range interaction in trapped ions: A. Sorensen, K. Molmer, "Multi-particle entanglement of hot trapped ions", Phys. Rev. Lett. 82, 1835 (1999).
Our proposal: P. Milman, W. Maineult, L. Guidoni, S. Guibal, B. Douçot, L. Ioffe, T. Coudreau, "Topologically decoherence-protected qubits with trapped ions", soumis, quant-ph/970702
If you very interest in learning more, it is also possible to join our group for a short stay or for a PhD (see the open positions'page).